I wanted to get proficient in Haskell so I decided to follow An [Essential] Haskell Reading List. There I stumbled upon Typoclassopedia, while the material is great, I couldn’t find solutions for the exercises to check against, so I decided I would write my own and hopefully the solutions would get fixed in case I have gone wrong by others. So if you think a solution is wrong, let me know in the comments!

In each section below, I left some reference material for the exercises and then the solutions.

Note: The post will be updated as I progress in Typoclassopedia myself

Functor

Instances

instance Functor [] where
  fmap :: (a -> b) -> [a] -> [b]
  fmap _ []     = []
  fmap g (x:xs) = g x : fmap g xs
  -- or we could just say fmap = map
 
instance Functor Maybe where
  fmap :: (a -> b) -> Maybe a -> Maybe b
  fmap _ Nothing  = Nothing
  fmap g (Just a) = Just (g a)

((,) e) represents a container which holds an “annotation” of type e along with the actual value it holds. It might be clearer to write it as (e,), by analogy with an operator section like (1+), but that syntax is not allowed in types (although it is allowed in expressions with the TupleSections extension enabled). However, you can certainly think of it as (e,).

((->) e) (which can be thought of as (e ->); see above), the type of functions which take a value of type e as a parameter, is a Functor. As a container, (e -> a) represents a (possibly infinite) set of values of a, indexed by values of e. Alternatively, and more usefully, ((->) e) can be thought of as a context in which a value of type e is available to be consulted in a read-only fashion. This is also why ((->) e) is sometimes referred to as the reader monad; more on this later.

Exercises

Implement Functor instances for Either e and ((->) e).

Solution:

instance Functor (Either e) where
  fmap _ (Left e) = Left e
  fmap g (Right a) = Right (g a)
      
instance Functor ((->) e) where
  fmap g f = g . f

Implement Functor instances for ((,) e) and for Pair, defined as below. Explain their similarities and differences.

Solution:
```
instance Functor ((,) e) where
  fmap g (a, b) = (a, g b) 
      
      
data Pair a = Pair a a
instance Functor Pair where
  fmap g (Pair a b) = Pair (g a) (g b)
```
Their similarity is in the fact that they both represent types of two values. Their difference is that ((,) e) (tuples of two) can have values of different types (kind of (,) is * -> *) while both values of Pair have the same type a, so Pair has kind *.

Implement a Functor instance for the type ITree, defined as

 data ITree a = Leaf (Int -> a)
             | Node [ITree a]

Solution:

 instance Functor ITree where
   fmap g (Leaf f) = Leaf (g . f)
   fmap g (Node xs) = Node (fmap (fmap g) xs)

To test this instance, I defined a function to apply the tree to an Int:

 applyTree :: ITree a -> Int -> [a]
 applyTree (Leaf g) i = [g i]
 applyTree (Node []) _ = []
 applyTree (Node (x:xs)) i = applyTree x i ++ applyTree (Node xs) i

This is not a standard tree traversing algorithm, I just wanted it to be simple for testing.

Now test the instance:

 λ: let t = Node [Node [Leaf (+5), Leaf (+1)], Leaf (*2)]
 λ: applyTree t 1
 [6,2,2]
 λ: applyTree (fmap id t) 1
 [6,2,2]
 λ: applyTree (fmap (+10) t) 1
 [16, 12, 12]

Give an example of a type of kind * -> * which cannot be made an instance of Functor (without using undefined).

I don’t know the answer to this one yet!
Is this statement true or false?

The composition of two Functors is also a Functor.

If false, give a counterexample; if true, prove it by exhibiting some appropriate Haskell code.

Solution:

It’s true, and can be proved by the following function:
```
 ffmap :: (Functor f, Functor j) => (a -> b) -> f (j a) -> f (j b)
 ffmap g = fmap (fmap g)
```
You can test this on arbitrary compositions of Functors:
```
 main = do
   let result :: Maybe (Either String Int) = ffmap (+ 2) (Just . Right $ 5)
   print result -- (Just (Right 7))
```

Functor Laws

fmap id = id
fmap (g . h) = (fmap g) . (fmap h)

Exercises

Although it is not possible for a Functor instance to satisfy the first Functor law but not the second (excluding undefined), the reverse is possible. Give an example of a (bogus) Functor instance which satisfies the second law but not the first.

Solution:

This is easy, consider this instance:
```
 instance Functor [] where
   fmap _ [] = [1]
   fmap g (x:xs) = g x: fmap g xs
```
Then, you can test the first and second laws:
```
 λ: fmap id [] -- [1], breaks the first law
 λ: fmap ((+1) . (+2)) [1,2] -- [4, 5], second law holds
 λ: fmap (+1) . fmap (+2) $ [1,2] -- [4, 5]
```
Which laws are violated by the evil Functor instance for list shown above: both laws, or the first law alone? Give specific counterexamples.
```
 -- Evil Functor instance
 instance Functor [] where
   fmap :: (a -> b) -> [a] -> [b]
   fmap _ [] = []
   fmap g (x:xs) = g x : g x : fmap g xs
```
Solution:

The instance defined breaks the first law (fmap id [1] -- [1,1]), but holds for the second law.

Category Theory

The Functor section links to Category Theory, so here I’m going to cover the exercises of that page, too.

Introduction to categories

Category laws:

The compositions of morphisms need to be associative:

$f \circ (g \circ h) = (f \circ g) \circ h$
The category needs to be closed under the composition operator. So if $f

B \to C$ and $g: A \to B$, then there must be some $h: A \to C$ in the category such that $h = f \circ g$.
Every object $A$ in a category must have an identity morphism, $id_A : A \to A$ that is an identity of composition with other morphisms. So for every morphism $g: A \to B$: $g \circ id_A = id_B \circ g = g$.

Exercises

As was mentioned, any partial order $(P, \leq)$ is a category with objects as the elements of P and a morphism between elements a and b iff $a \leq b$. Which of the above laws guarantees the transitivity of $\leq$?

Solution:

The second law, which states that the category needs to be closed under the composition operator guarantess that because we have a morphism $a \leq b$, and another morphism $b \leq c$, there must also be some other morphism such that $a \leq c$.
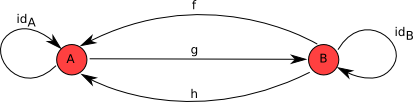
If we add another morphism to the above example, as illustrated below, it fails to be a category. Why? Hint: think about associativity of the composition operation.

Solution:

The first law does not hold:

$f \circ (g \circ h) = (f \circ g) \circ h$

To see that, we can evaluate each side to get an inequality:

$g \circ h = id_B$

$f \circ g = id_A$

$f \circ (g \circ h) = f \circ id_B = f$

$(f \circ g) \circ h = id_A \circ h = h$

$f \neq h$

Functors

Functor laws:

Given an identity morphism $id_A$ on an object $A$, $F(id_A)$ must be the identity morphism on $F(A)$, so: $F(id_A) = id_{F(A)}$
Functors must distribute over morphism composition: $F(f \circ g) = F(f) \circ F(g)$

Exercises

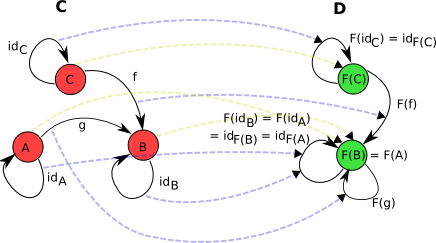
Check the functor laws for the diagram below.

Solution:

The first law is obvious as it’s directly written, the pale blue dotted arrows from $id_C$ to $F(id_C) = id_{F(C)}$ and $id_A$ and $id_B$ to $F(id_A) = F(id_B) = id_{F(A)} = id_{F(B)}$ show this.

The second law also holds, the only compositions in category $C$ are between $f$ and identities, and $g$ and identities, there is no composition between $f$ and $g$.

(Note: The second law always hold as long as the first one does, as was seen in Typoclassopedia)

Check the laws for the Maybe and List functors.

Solution:

 instance Functor [] where
   fmap :: (a -> b) -> [a] -> [b]
   fmap _ []     = []
   fmap g (x:xs) = g x : fmap g xs
    
 -- check the first law for each part:
 fmap id [] = []
 fmap id (x:xs) = id x : fmap id xs = x : fmap id xs -- the first law holds recursively
    
 -- check the second law for each part:
 fmap (f . g) [] = []
 fmap (f . g) (x:xs) = (f . g) x : fmap (f . g) xs = f (g x) : fmap (f . g) xs
 fmap f (fmap g (x:xs)) = fmap f (g x : fmap g xs) = f (g x) : fmap (f . g) xs

 instance Functor Maybe where
   fmap :: (a -> b) -> Maybe a -> Maybe b
   fmap _ Nothing  = Nothing
   fmap g (Just a) = Just (g a)
    
 -- check the first law for each part:
 fmap id Nothing = Nothing
 fmap id (Just a) = Just (id a) = Just a
    
 -- check the second law for each part:
 fmap (f . g) Nothing = Nothing
 fmap (f . g) (Just x) = Just ((f . g) x) = Just (f (g x))
 fmap f (fmap g (Just x)) = Just (f (g x)) = Just ((f . g) x)

Applicative

Laws

The identity law:
```
 pure id <*> v = v
```
Homomorphism:
```
 pure f <*> pure x = pure (f x)
```
Intuitively, applying a non-effectful function to a non-effectful argument in an effectful context is the same as just applying the function to the argument and then injecting the result into the context with pure.
Interchange:
```
 u <*> pure y = pure ($ y) <*> u
```
Intuitively, this says that when evaluating the application of an effectful function to a pure argument, the order in which we evaluate the function and its argument doesn’t matter.
Composition:
```
 u <*> (v <*> w) = pure (.) <*> u <*> v <*> w
```
This one is the trickiest law to gain intuition for. In some sense it is expressing a sort of associativity property of (<*>). The reader may wish to simply convince themselves that this law is type-correct.

Exercises

(Tricky) One might imagine a variant of the interchange law that says something about applying a pure function to an effectful argument. Using the above laws, prove that

pure f <*> x = pure (flip ($)) <*> x <*> pure f

Solution:

pure (flip ($)) <*> x <*> pure f
  = (pure (flip ($)) <*> x) <*> pure f -- <*> is left-associative
  = pure ($ f) <*> (pure (flip ($)) <*> x) -- interchange
  = pure (.) <*> pure ($ f) <*> pure (flip ($)) <*> x -- composition
  = pure (($ f) . (flip ($))) <*> x -- homomorphism
  = pure ((flip ($) f) . (flip ($))) <*> x -- identical
  = pure f <*> x

Explanation of the last transformation:

flip ($) has type a -> (a -> c) -> c, intuitively, it first takes an argument of type a, then a function that accepts that argument, and in the end it calls the function with the first argument. So (flip ($) 5) takes as argument a function which gets called with 5 as it’s argument. If we pass (+ 2) to (flip ($) 5), we get (flip ($) 5) (+2) which is equivalent to the expression (+2) $ 5, evaluating to 7.

flip ($) f is equivalent to \x -> x $ f, that means, it takes as input a function and calls it with the function f as argument.

The composition of these functions works like this: First flip ($) takes x as it’s first argument, and returns a function (flip ($) x), this function is awaiting a function as it’s last argument, which will be called with x as it’s argument. Now this function (flip ($) x) is passed to flip ($) f, or to write it’s equivalent (\x -> x $ f) (flip ($) x), this results in the expression (flip ($) x) f, which is equivalent to f $ x.

You can check the type of (flip ($) f) . (flip ($)) is something like this (depending on your function f):

λ: let f = sqrt
λ: :t (flip ($) f) . (flip ($))
(flip ($) f) . (flip ($)) :: Floating c => c -> c

Also see this question on Stack Overflow which includes alternative proofs.

Instances

Applicative instance of lists as a collection of values:

newtype ZipList a = ZipList { getZipList :: [a] }
 
instance Applicative ZipList where
  pure :: a -> ZipList a
  pure = undefined   -- exercise
 
  (<*>) :: ZipList (a -> b) -> ZipList a -> ZipList b
  (ZipList gs) <*> (ZipList xs) = ZipList (zipWith ($) gs xs)

Applicative instance of lists as a non-deterministic computation context:

instance Applicative [] where
  pure :: a -> [a]
  pure x = [x]
 
  (<*>) :: [a -> b] -> [a] -> [b]
  gs <*> xs = [ g x | g <- gs, x <- xs ]

Exercises

Implement an instance of Applicative for Maybe.

Solution:

 instance Applicative (Maybe a) where
   pure :: a -> Maybe a
   pure x = Just x
      
   (<*>) :: Maybe (a -> b) -> Maybe a -> Maybe b
   _ <*> Nothing = Nothing
   Nothing <*> _ = Nothing
   (Just f) <*> (Just x) = Just (f x)

Determine the correct definition of pure for the ZipList instance of Applicative—there is only one implementation that satisfies the law relating pure and (<*>).

Solution:

 newtype ZipList a = ZipList { getZipList :: [a] }
    
 instance Functor ZipList where
   fmap f (ZipList list) = ZipList { getZipList = fmap f list }
    
 instance Applicative ZipList where
   pure = ZipList . pure
    
   (ZipList gs) <*> (ZipList xs) = ZipList (zipWith ($) gs xs)

You can check the Applicative laws for this implementation.

Utility functions

Exercises

Implement a function sequenceAL :: Applicative f => [f a] -> f [a] There is a generalized version of this, sequenceA, which works for any Traversable (see the later section on Traversable), but implementing this version specialized to lists is a good exercise.

Solution:
```
 createList = replicate 1

 sequenceAL :: Applicative f => [f a] -> f [a]
 sequenceAL = foldr (\x b -> ((++) . createList <$> x) <*> b) (pure [])
```
Explanation:

First, createList is a simple function for creating a list of a single element, e.g. createList 2 == [2].

Now let’s take sequenceAL apart, first, it does a fold over the list [f a], and b is initialized to pure [], which results in f [a] as required by the function’s output.

Inside the function, createList <$> x applies createList to the value inside f a, resulting in f [a], and then (++) is applied to the value again, so it becomes f ((++) [a]), now we can apply the function (++) [a] to b by ((++) . createList <$> x) <*> b, which results in f ([a] ++ b).

Alternative formulation

Definition

class Functor f => Monoidal f where
  unit :: f ()
  (**) :: f a -> f b -> f (a,b)

Laws:

Left identity
```
 unit ** v ≅ v
```
Right identity
```
 u ** unit ≅ u
```
Associativity
```
 u ** (v ** w) ≅ (u ** v) ** w
```

Neutrality

 fmap (g *** h) (u ** v) = fmap g u ** fmap h v

Isomorphism

In the laws above, ≅ refers to isomorphism rather than equality. In particular we consider:

(x,()) ≅ x ≅ ((),x)
((x,y),z) ≅ (x,(y,z))

Exercises

Implement pure and <*> in terms of unit and **, and vice versa.

 unit :: f ()
 unit = pure ()
    
 (**) :: f a -> f b -> f (a, b)
 a ** b = fmap (,) a <*> b
    
 pure :: a -> f a
 pure x = unit ** x
    
 (<*>) :: f (a -> b) -> f a -> f b
 f <*> a = fmap (uncurry ($)) (f ** a) = fmap (\(f, a) -> f a) (f ** a)

Are there any Applicative instances for which there are also functions f () -> () and f (a,b) -> (f a, f b), satisfying some “reasonable” laws?

The Arrow type class seems to satisfy these criteria.
```
   first unit = ()
      
   (id *** f) (a, b) = (f a, f b)
```

(Tricky) Prove that given your implementations from the first exercise, the usual Applicative laws and the Monoidal laws stated above are equivalent.

Identity Law

 pure id <*> v
   = fmap (uncurry ($)) ((unit ** id) ** v)
   = fmap (uncurry ($)) (id ** v)
   = fmap id v
   = v

Homomorphism

 pure f <*> pure x
   = (unit ** f) <*> (unit ** x)
   = fmap (\(f, a) -> f a) (unit ** f) (unit ** x)
   = fmap (\(f, a) -> f a) (f ** x)
   = fmap f x
   = pure (f x)

Interchange

 u <*> pure y
   = fmap (uncurry ($)) (u ** (unit ** y))
   = fmap (uncurry ($)) (u ** y)
   = fmap (u $) y
   = fmap ($ y) u
   = pure ($ y) <*> u

Composition

 u <*> (v <*> w)
   = fmap (uncurry ($)) (u ** (fmap (uncurry ($)) (v ** w)))
   = fmap (uncurry ($)) (u ** (fmap v w))
   = fmap u (fmap v w)
   = fmap (u . v) w
   = pure (.) <*> u <*> v <*> w =

Monad

Definition

class Applicative m => Monad m where
  return :: a -> m a
  (>>=)  :: m a -> (a -> m b) -> m b
  (>>)   :: m a -> m b -> m b
  m >> n = m >>= \_ -> n
 
  fail   :: String -> m a

Instances

instance Monad Maybe where
  return :: a -> Maybe a
  return = Just
 
  (>>=) :: Maybe a -> (a -> Maybe b) -> Maybe b
  (Just x) >>= g = g x
  Nothing  >>= _ = Nothing

Exercises

Implement a Monad instance for the list constructor, []. Follow the types!

Solution:

 instance Monad [] where
   return a = [a]
      
   [] >> _ = []
   (x:xs) >>= f = f x : xs >>= f

Implement a Monad instance for ((->) e).

Solution:

 instance Monad ((->) e) where
   return x = const x
      
   g >>= f = f . g

Implement Functor and Monad instance for Free f, defined as:

 data Free f a = Var a
               | Node (f (Free f a))

You may assume that f has a Functor instance. This is known as the free monad built from the functor f.

Solution:

 instance Functor (Free f) where
   fmap f (Var a) = Var (f a)
   fmap f (Node x) = Node (f x)
      
 instance Monad (Free f) where
   return x = Var x
      
   (Var x) >>= f = Var (f x)
   (Node x) >>= f = Node (fmap f x)

Intuition

Exercises

Implement (>>=) in terms of fmap (or liftM) and join.

Solution:
```
 a >>= f = join (fmap f a)
```

Now implement join and fmap (liftM) in terms of (>>=) and return.

Solution:

 fmap f a = a >>= (return . f)
 join m = m >>= id

Laws

Standard:

return a >>= k  =  k a
m >>= return    =  m
m >>= (\x -> k x >>= h)  =  (m >>= k) >>= h

In terms of >=>:

return >=> g  =  g
g >=> return  =  g
(g >=> h) >=> k  =  g >=> (h >=> k)

Exercises

Given the definition g >=> h = \x -> g x >>= h, prove the equivalence of the above laws and the standard monad laws.

Solution:

 return >=> g
   = \x -> return x >>= g
   = \x -> g x
   = g
      
 g >=> return
   = \x -> g x >>= return
   = \x -> g x
   = g
    
 g >=> (h >=> k)
   = \y -> g y >>= (\x -> h x >>= k)
   = \y -> (g y >>= h) >>= k
   = \y -> (\x -> g x >>= h) y >>= k
   = (\x -> g x >>= h) >=> k
   = (g >=> h) >=> k

Monad Transformers

Definition and laws

class MonadTrans t where
  lift :: Monad m => m a -> t m a

Exercises

What is the kind of t in the declaration of MonadTrans?

Solution:

t is of the kind (* -> *) -> * -> *, as we see in (t m) a, t accepts a Monad first, which is of type * -> *, and then another argument of kind *.

Composing Monads

Exercises

Implement join :: M (N (M (N a))) -> M (N a) given distrib :: N (M a) -> M (N a) and assuming M and N are instances of Monad.

 join :: M (N (M (N a))) -> M (N a)
 join m = distrib ((distrib m) >>= join) >>= join
    
 -- one by one
 let m :: M (N (M (N a)))
     a = distrib m  :: N (M (M (N a)))
     b = a >>= join :: N (M (N a))
     c = distrib b  :: M (N (N a))
 in c >>= join      :: M (N a)

MonadFix

Examples and intuition

maybeFix :: (a -> Maybe a) -> Maybe a
maybeFix f = ma
  where ma = f (fromJust ma)

Exercises

Implement a MonadFix instance for [].

Solution:

 listFix :: (a -> [a]) -> [a]
 listFix f = la
   where la = f (head la)

Foldable

Definition

class Foldable t where
  fold    :: Monoid m => t m -> m
  foldMap :: Monoid m => (a -> m) -> t a -> m
  foldr   :: (a -> b -> b) -> b -> t a -> b
  foldr'  :: (a -> b -> b) -> b -> t a -> b
  foldl   :: (b -> a -> b) -> b -> t a -> b
  foldl'  :: (b -> a -> b) -> b -> t a -> b
  foldr1  :: (a -> a -> a) -> t a -> a
  foldl1  :: (a -> a -> a) -> t a -> a
  toList  :: t a -> [a]
  null    :: t a -> Bool
  length  :: t a -> Int
  elem    :: Eq a => a -> t a -> Bool
  maximum :: Ord a => t a -> a
  minimum :: Ord a => t a -> a
  sum     :: Num a => t a -> a
  product :: Num a => t a -> a

Instances and examples

Exercises

Implement fold in terms of foldMap.

Solution:
```
 fold = foldMap id
```
What would you need in order to implement foldMap in terms of fold?

Solution:

A map function should exist for the instance, so we can apply the function (a -> m) to the container first.
```
 foldMap f = fold . map f
```

Implement foldMap in terms of foldr.

Solution:

 foldMap f = foldr (\a b -> mappend (f a) b) mempty

Implement foldr in terms of foldMap (hint: use the Endo monoid).

Solution:
```
 foldr f b c = foldMap (Endo . f) c `appEndo` b
```

What is the type of foldMap . foldMap? Or foldMap . foldMap . foldMap, etc.? What do they do?

Solution:

Each composition makes foldMap operate on a deeper level, so:

 foldMap :: Monoid m => (a -> m) -> t a -> m
 foldMap . foldMap :: Monoid m => (a -> m) -> t (t a) -> m
 foldMap . foldMap . foldMap :: Monoid m => (a -> m) -> t (t (t a)) -> m
    
 foldMap id [1,2,3] :: Sum Int -- 6
 (foldMap . foldMap) id [[1,2,3]] :: Sum Int -- 6
 (foldMap . foldMap . foldMap) id [[[1,2,3]]] :: Sum Int -- 6

Derived folds

Exercises

Implement toList :: Foldable f => f a -> [a] in terms of either foldr or foldMap.

Solution:
```
 toList = foldMap (replicate 1)
```
Show how one could implement the generic version of foldr in terms of toList, assuming we had only the list-specific foldr :: (a -> b -> b) -> b -> [a] -> b.

Solution:
```
 foldr f b c = foldr f b (toList c)
```

Pick some of the following functions to implement: concat, concatMap, and, or, any, all, sum, product, maximum(By), minimum(By), elem, notElem, and find. Figure out how they generalize to Foldable and come up with elegant implementations using fold or foldMap along with appropriate Monoid instances.

Solution:

 concat :: Foldable t => t [a] -> [a]
 concat = foldMap id
    
 concatMap :: Foldable t => (a -> [b]) -> t a -> [b]
 concatMap f = foldMap (foldMap (replicate 1 . f))
    
 and :: Foldable t => t Bool -> Bool
 and = getAll . foldMap All
    
 or :: Foldable t => t Bool -> Bool
 or = getAny . foldMap Any
      
 any :: Foldable t => (a -> Bool) -> t a -> Bool
 any f = getAny . foldMap (Any . f)
    
 all :: Foldable t => (a -> Bool) t a -> Bool
 all f = getAll . foldMap (All . f)
    
 sum :: (Num a, Foldable t) => t a -> a
 sum = getSum . foldMap Sum
    
 product :: (Num a, Foldable t) => t a -> a
 product = getProduct . foldMap Product
    
 -- I think there are more elegant implementations for maximumBy, leave a comment
 -- if you have a suggestion
 maximumBy :: Foldable t => (a -> a -> Ordering) -> t a -> a
 maximumBy f c = head $ foldMap (\a -> [a | cmp a]) c
   where
     cmp a = all (/= LT) (map (f a) lst)
     lst = toList c
    
 elem :: (Eq a, Foldable t) => a -> t a -> Bool
 elem x c = any (==x) c
    
 find :: Foldable t => (a -> Bool) -> t a -> Maybe a 
 find f c = listToMaybe $ foldMap (\a -> [a | f a]) c 

Utility functions

sequenceA_ :: (Applicative f, Foldable t) => t (f a) -> f () takes a container full of computations and runs them in sequence, discarding the results (that is, they are used only for their effects). Since the results are discarded, the container only needs to be Foldable. (Compare with sequenceA :: (Applicative f, Traversable t) => t (f a) -> f (t a), which requires a stronger Traversable constraint in order to be able to reconstruct a container of results having the same shape as the original container.)
traverse_ :: (Applicative f, Foldable t) => (a -> f b) -> t a -> f () applies the given function to each element in a foldable container and sequences the effects (but discards the results).

Exercises

Implement traverse_ in terms of sequenceA_ and vice versa. One of these will need an extra constraint. What is it?

Solution:

 sequenceA_ :: (Applicative f, Foldable t) => t (f a) -> f ()
 sequenceA_ = traverse_ id
    
 traverse_ :: (Applicative f, Foldable t, Functor t) => (a -> f b) -> t a -> f ()
 traverse_ f c = sequenceA_ (fmap f c)

The additional constraint for implementing traverse_ in terms of sequenceA_ is the requirement of the Foldable instance t to be a Functor as well.

Traversable

Intuition

traverse :: Applicative f => (a -> f b) -> t a -> f (t b)
sequenceA :: Applicative f => t (f a) -> f (t a)

Exercises

There are at least two natural ways to turn a tree of lists into a list of trees. What are they, and why?

Note: I’m not really sure whether my solution is natural, I think the question is rather ambiguous in the sense that it’s not clear whether the trees in the final list of trees can have lists as their values, i.e. Tree [Int] -> [Tree [Int]] is valid or only Tree [Int] -> [Tree Int] is, but let me know if you think otherwise.

Solution:

One way is to put each Node, Leaf or Empty in a list in-order, this way the structure of the tree can be recovered from the list, here is a quick sketch ([] is an arbitrary list):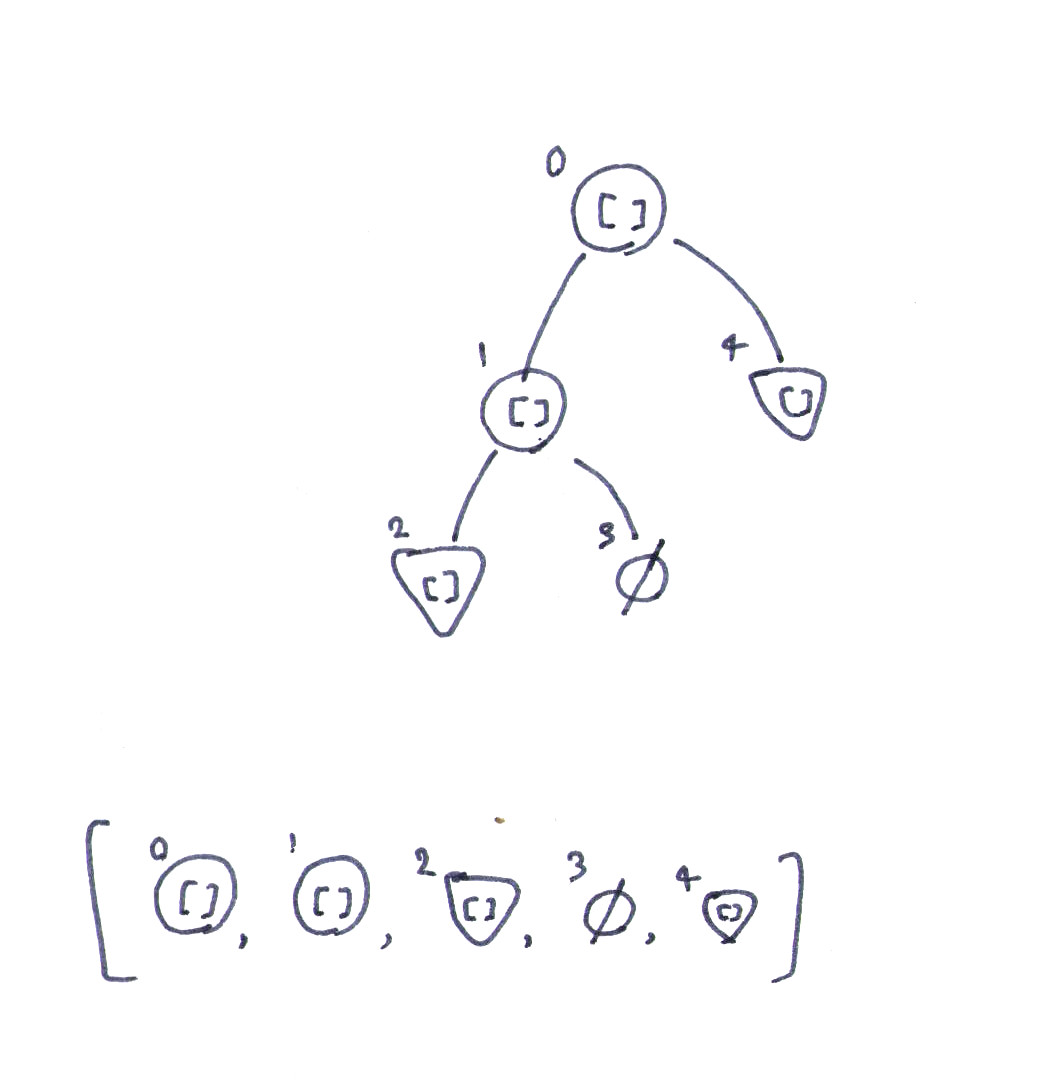
```
 let tree = Node (Node (Leaf []) Empty) [] (Leaf [])
 let list = [Node Empty [] Empty, Node Empty [] Empty, Leaf [], Empty, Leaf []]
```
Give a natural way to turn a list of trees into a tree of lists.

Solution:

To recover the original tree from the list of trees, whenever we encounter a Node in the list, we catch the next three values as left, value, and right nodes of the original node.
What is the type of traverse . traverse? What does it do?

Solution:
```
 (traverse . traverse) :: Applicative f => (a -> f b) -> t (t2 a) -> f (t (t2 b))
```
It traverses on a deeper level, retaining the structure of the first level.

Implement traverse in terms of sequenceA, and vice versa.

Solution:

 sequenceA = traverse id
    
 traverseA f c = sequenceA (fmap f c)

Instances and examples

Exercises

Implement fmap and foldMap using only the Traversable methods. (Note that the Traversable module provides these implementations as fmapDefault and foldMapDefault.)

Solution:

 newtype Id a = Id { getId :: a }
    
 instance Functor Id where
   fmap f (Id x) = Id (f x)
    
 instance Applicative Id where
   pure x = Id x
   (Id f) <*> (Id x) = Id (f x)
    
 fmapDefault :: Traversable t => (a -> b) -> t a -> t b
 fmapDefault f = getId . traverse (Id . f)
    
 foldMapDefault :: (Monoid m, Traversable t) => (a -> m) -> t a -> m
 foldMapDefault f = getConst . traverse (Const . f)

See the Const Functor’s definition for intuition.

Implement Traversable instances for [], Maybe, ((,) a), and Either a.

Solution:

 instance Traversable [] where
   traverse :: Applicative f => (a -> f b) -> [a] -> f [b]
   traverse _ [] = pure []
   traverse f (x:xs) = (:) <$> f x <*> Main.traverse f xs
      
 instance Traversable Maybe where
   traverse :: Applicative f => (a -> f b) -> Maybe a -> f (Maybe b)
      
   traverse _ Nothing = pure Nothing
   traverse f (Just x) = Just <$> f x
      
 instance Traversable ((,) c) where
   traverse :: Applicative f => (a -> f b) -> (c, a) -> f (c, b)
      
   traverse f (c, a) = (,) c <$> f a
      
 instance Traversable (Either c) where
   traverse :: Applicative f => (a -> f b) -> Either c a -> f (Either c b)
      
   traverse _ (Left c) = pure (Left c)
   traverse f (Right a) = Right <$> f a

Explain why Set is Foldable but not Traversable.

Solution:

First, in terms of laws, Set is not a Functor, thus it cannot be made into a Traversable instance, since Traversable instances require Functor superclasses.

Second, on an intuitive level: In Foldable, the goal is not to keep the shape/structure of the original container, we are trying to reduce the container into some value, and the shape of the final result doesn’t matter, but in Traversable, we ought to keep the structure of the final result, but we can’t guarantee this while using Sets, because we can define some transformation f :: Set a -> Set a which reduces the length of the Set.

See Foldable vs. Traversable and Sets, Functors and Eq confusion. and Foldable and Traversable for more details.

Show that Traversable functors compose: that is, implement an instance for Traversable (Compose f g) given Traversable instances for f and g.

Solution:

 instance (Traversable f, Traversable g) => Traversable (Compose f g) where
   traverse :: (Applicative f) => (a -> f b) -> Compose g h a -> f (Compose g h b)
   traverse f (Compose t) = Compose <$> traverse (traverse f) t

Table of Contents

Functor

Instances

Exercises

Functor Laws

Exercises

Category Theory

Introduction to categories

Category laws:

Exercises

Functors

Functor laws:

Exercises

Applicative

Laws

Exercises

Instances

Exercises

Utility functions

Exercises

Alternative formulation

Definition

Laws:

Isomorphism

Exercises

Monad

Definition

Instances

Exercises

Intuition

Exercises

Laws

Exercises

Monad Transformers

Definition and laws

Exercises

Composing Monads

Exercises

MonadFix

Examples and intuition

Exercises

Foldable

Definition

Instances and examples

Exercises

Derived folds

Exercises

Utility functions

Exercises

Traversable

Intuition

Exercises

Instances and examples

Exercises